JAX でポアソン方程式を解く¶

JAXで、以下のポアソン方程式を周期境界条件で解きます。

\[ \frac{\partial^2 p}{\partial x^2} + \frac{\partial^2 p}{\partial y^2} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \]

\[\begin{split} u = \sin 2 x \\ v = \sin 2 y \end{split}\]

コードは以下の通り。

### CPU で実行する場合は、以下二行をコメントアウトする。
# from jax import config
# config.update('jax_platform_name', 'cpu')

import jax.numpy as jnp
from jax.numpy import pi
from jax.numpy import gradient
from jax.scipy.sparse.linalg import bicgstab, gmres
from jax import jit
from functools import partial

class poisson_jax(object):
    def __init__(self, nx, ny, lx=2*pi, ly=2*pi):
        self.nx = nx
        self.ny = ny
        self.lx = lx
        self.ly = ly
        self.dx = self.lx / self.nx
        self.dy = self.ly / self.ny

    def dfdx(self, f):
        f_ = jnp.pad(f, pad_width=1, mode='wrap')
        return gradient(f_, self.dx, axis=-1)[1:-1,1:-1]

    def dfdy(self, f):
        f_ = jnp.pad(f, pad_width=1, mode='wrap')
        return gradient(f_, self.dy, axis=-2)[1:-1,1:-1]

    def lhs(self, p_flatten):
        p = p_flatten.reshape((self.ny, self.nx))
        ddp = self.dfdx(self.dfdx(p)) + self.dfdy(self.dfdy(p))
        return ddp.flatten()

    def rhs(self, u, v):
        return (self.dfdx(u) + self.dfdy(v)).flatten()

    def solve(self, u, v):
        p_flatten, _ = bicgstab(A=self.lhs, b=self.rhs(u, v))
        # p_flatten, _ = gmres(A=self.lhs, b=self.rhs(u, v))
        return p_flatten.reshape((self.ny, self.nx))

    @partial(jit, static_argnums=0)
    def solve_jit(self, u, v):
        return self.solve(u, v)

動作確認¶

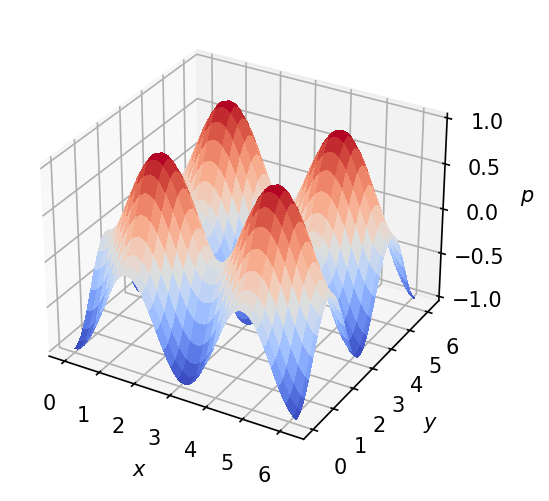
解いてみると、以下のように圧力の空間分布が得られました。
空間分割数を大きくすると、GMRES法が収束しませんでした。理由はわかっていません。

nx = ny = 64
lx = ly = 2 * pi

x = jnp.linspace(0, lx, nx, endpoint=False)
y = jnp.linspace(0, ly, ny, endpoint=False)
X, Y = jnp.meshgrid(x, y)

u = jnp.sin(2*X)
v = jnp.sin(2*Y)

solver = poisson_jax(nx, ny, lx, ly)
p = solver.solve(u, v).block_until_ready()

import matplotlib.pyplot as plt
from matplotlib import cm

fig, ax = plt.subplots(subplot_kw={"projection": "3d"}, dpi=150)
ax.plot_surface(X, Y, p, cmap=cm.coolwarm, linewidth=0, antialiased=False)
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.set_zlabel("$p$")
plt.show()

計算時間を計測¶

配列の大きさとJITコンパイルの有無を変えて計測します。

# for n in range(5, 14):
#     nx = ny = 2 ** n
#     lx = ly = 2 * pi

#     x = jnp.linspace(0, lx, nx, endpoint=False)
#     y = jnp.linspace(0, ly, ny, endpoint=False)
#     X, Y = jnp.meshgrid(x, y)

#     u = jnp.sin(2*X)
#     v = jnp.sin(2*Y)

#     solver = poisson_jax(nx, ny, lx, ly)

#     print(f'nx = ny = {nx}')

#     print('uncompiled')
#     %timeit solver.solve(u, v).block_until_ready()

#     print('JIT-compiled')
#     %timeit solver.solve_jit(u, v).block_until_ready()

技術メモ

JAX でポアソン方程式を解く

Contents

JAX でポアソン方程式を解く¶

動作確認¶

計算時間を計測¶